數據分析與討論
「相對的密度」比較下,較大的溶液滴入於密度較小的溶液中,會產生環狀的密度流現象()。此環狀密度流在液體中沿著重力方向越降速度越慢。在運動中,其初入水面時到完全散逸的形態依序是:
|
1. 未入水前的水滴狀 |
↓
|
2. 初入水,保持水滴狀 |
↓
|
3. 環形渦流中心呈現凹陷,底部微凸的杯狀 |
↓
|
4. 環形渦流中心承受不了來自上方的外力而貫穿形成環狀 |
↓
|
5. 環形渦流的外環越往下越大,而速度則呈現沿著重力方向越降速度越慢的運動形式,環形渦流的壁高則由小漸增 |
↓
|
6. 環流被拉扯致極限時,環流被迫再分裂成數個微小的環流 |
↓
|
7. 數個微小的環流維持1/30s秒左右,終致散開呈現無序的紊流而消失 |
分析流場流向及受力情形
:環形渦流由滯留→散逸大環期間,在產生滯留後,由於中心部份上下水流相激,衝裂了環流。而每段裂的環流又因表面張力影響,又形成球狀下降,進而又在次變成微小的環流。
﹙二﹚分析距離水面上
5mm、0mm環流速度與討論1.
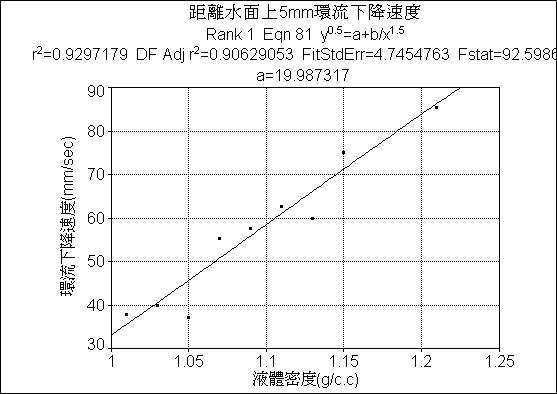
模擬距離水面上5mm環流下降速度簡單線性程式圖
(6.2.1)
分析距離水面上
5mm環流下降速度:由TableCurve2D繪出簡單線性模擬程式中,看出環流下降速度與液體密度有明顯成正比的關係。誤差值
:相差甚小,可信度很高。
2.
模擬距離水面上0mm環流下降速度簡單線性程式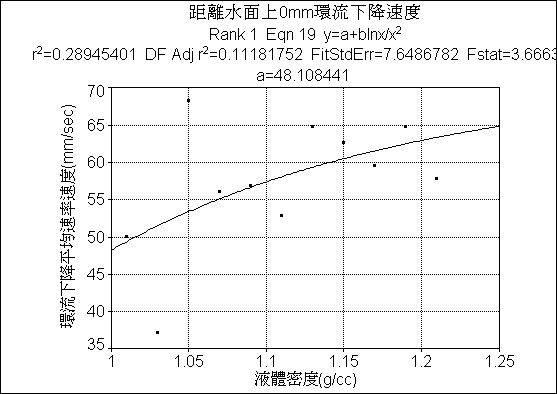
分析距離水面上
0mm環流下降速度:由TableCurve2D繪出簡單線性模擬程式中,由於1.03、1.05兩點起伏太大影響模擬程式,所以懷疑這兩點為誤差值。整體上環流下降速度與液體密度成正比的關係,曲線斜率比距離水面上5mm環流下降速度小。誤差值
:由於1.03、1.05兩點起伏太大影響,造成誤差值變大。3.
討論:液滴距離水面上高度
5mm、0mm處滴落,對環流有相當明顯的差別。由圖比較得出,兩條曲線會有交點。而距離水面的高度
5mm的曲線受到空氣阻力、表面張力及重力位能產生的動能的影響,推論在交點之前空氣阻力、表面張力(液滴與水面接觸時,造成水與鹽水的表面張力會互相排斥產生阻力)的影響大於重力位能產生的動能,所以形成頻率及速度特別低,在交點之後重力位能產生的動能影響大於空氣阻力、表面張力,所以速度提高趕過距離水面的高度0mm環流(沒有重力位能產生的動能),但是形成頻率還是比距離水面的高度0mm環流低太多(受表面張力影響)。
(
三)分析距離水面上0mm環流速度、放大率、散逸時間、維持時間與討論P
.S: 距離水面上5mm環流速度、放大率、散逸時間會有空氣阻力的問題,所以不做討論。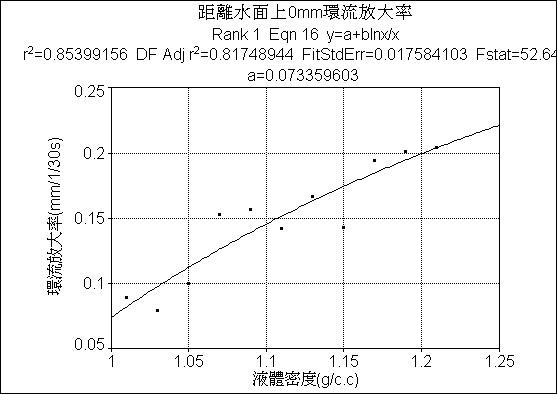
圖
(6.3.1)分析距離水面上
0mm環流放大率:由TableCurve2D繪出簡單線性模擬程式中,1.07、1.15雖在誤差線之外,但影響不大。整體上環流放大率與液體密度成正比的關係。誤差值
:1.07、1.15雖在誤差線之外,但誤差值相差甚小,可信度很高。附環流放大率折線圖與數據表
2.
模擬距離水面上0mm環流散逸時間簡單線性程式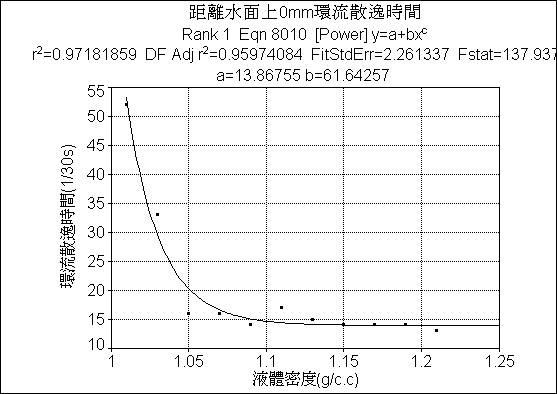
圖
(6.3.2)分析距離水面上
0mm環流散逸時間:由TableCurve2D繪出簡單線性模擬程式中,環流散逸時間曲線趨近終端,所有點都在誤差曲線內。誤差值
:誤差值極小,可信度很高。附
環流散逸時間折線圖與數據表
3.
模擬距離水面上0mm環流維持時間簡單線性程式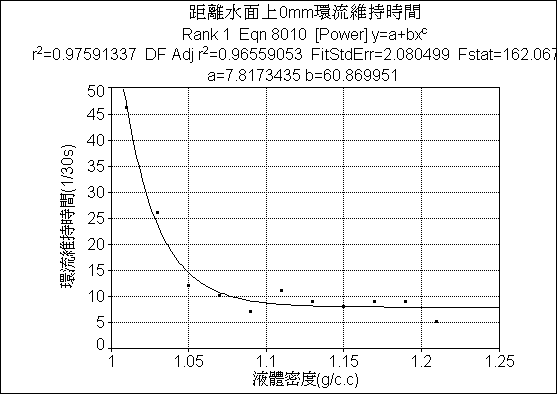
分析距離水面上
0mm環流維持時間:由TableCurve2D繪出簡單線性模擬程式中,環流維持時間曲線也趨近終端,與環流散逸時間曲線為同一條線性程式。誤差值
:誤差值極小,可信度很高。附
環流維持時間折線圖與數據表
4.
討論:距離水面的高度
0mm的環流放大率圖、散逸時間圖、環流維持時間、速率圖可以推得速率越快,放大率則越大(正好可以說明Bernoulli定律中的速率差值大小,所造成壓力差大小控制外直徑大小),又因每1/30S放大率有變大的趨勢,所以散逸時間會越來越快(因為外環為有限制擴大,超過極限則碎裂散逸,也因為外環擴大,造成上下水流流場相激衝散了環流)。
﹙四﹚分析不同密度下環流外直徑、內直徑、壁高、壁厚
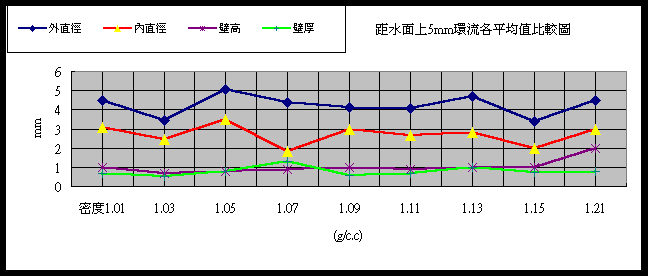
1.
距離水面上5mm環流外直徑、內直徑、壁高、壁厚折線圖 圖﹙6.4.1﹚外直徑
:1.03、1.15為所有外直徑最低點,1.05、1.13為所有外直徑最高點,其餘各點則相差不大,折線圖形呈現近似波浪狀。內直徑
:折線圖形與外直徑相似。壁高
:折線圖形有逐漸變大的趨勢。壁厚
(外直徑-內直徑):各點值相差甚小,折線圖形呈現近似一直線。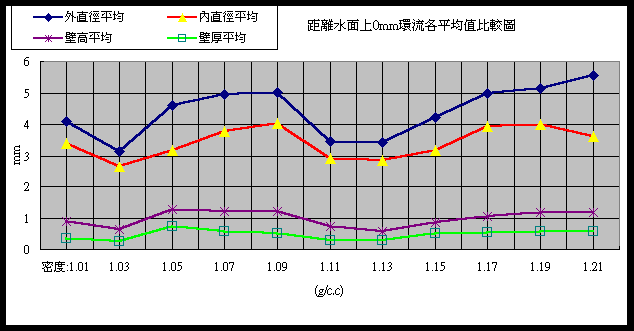
2.
距離水面上0mm環流外直徑、內直徑、壁高、壁厚折線圖 圖﹙6.4.2﹚外直徑、內直徑、壁高、壁後
:這四者折線圖形非常相似。附數據表